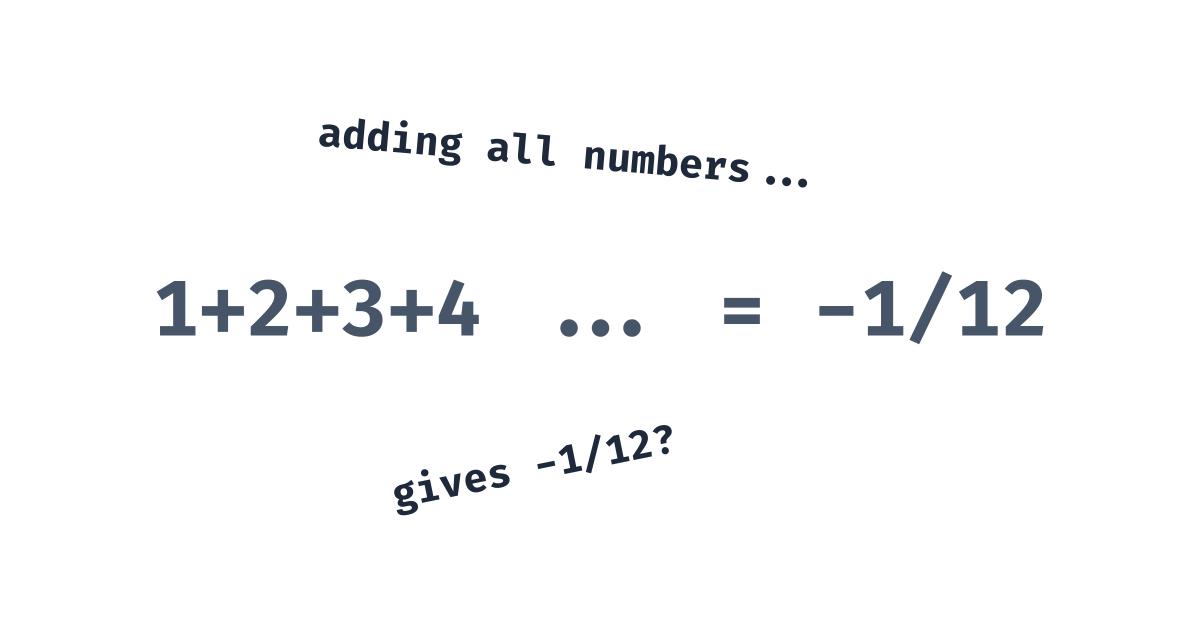Infinity is -1/12

Proof that 1 + 2 + 3 + 4 ... = -1/12.

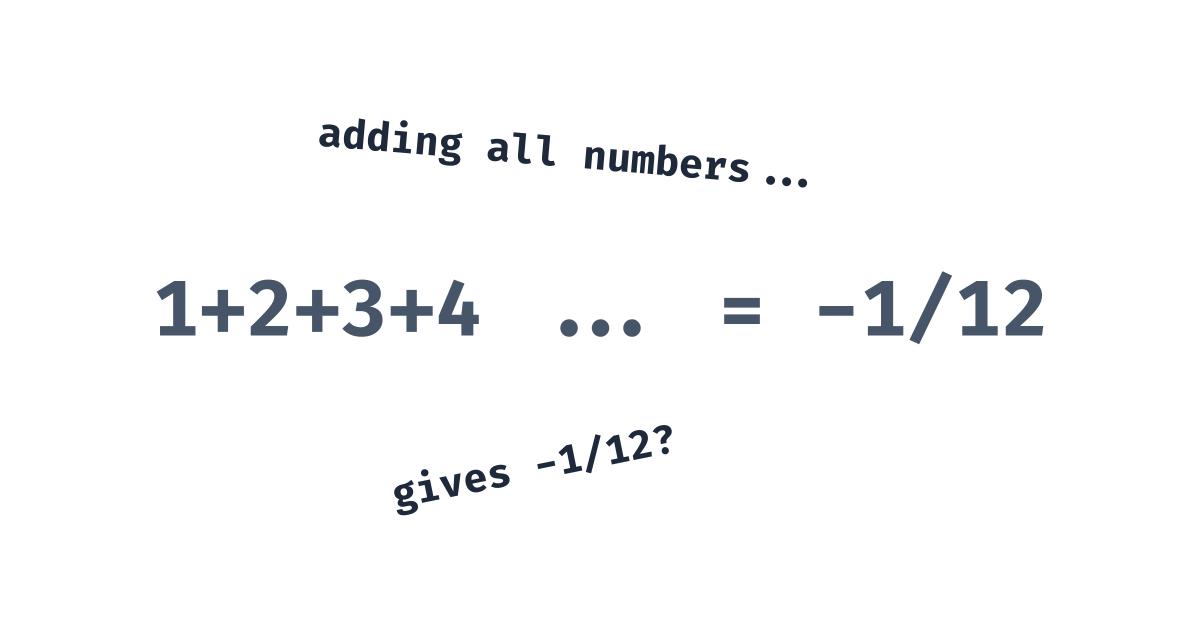
Did you know that the sum of all whole numbers is equal to -1/12? In this article we find out how it’s possible and prove it ourselves using simple algebra and math!

DISCLAIMER: The math used in this article doesn’t count as real reasoning; it’s just a fun thing to think about. See this video by Mathologer for more information.

The Series

We will define three series that we need to find out: $S$ , $G$ , and $H$ .

\begin{aligned} S &= 1 + 2 + 3 + 4 + 5 + ... \\ G &= 1 - 1 + 1 - 1 + 1 - ... \\ H &= 1 - 2 + 3 - 4 + 5 - ... \\ \end{aligned}

Solving for G

Our base step is to solve $G$ . This is pretty simple:

\begin{aligned} G &= 1 - 1 + 1 - 1 + 1 ... \\ G &= 1 - (1 - 1 + 1 - 1 ...) \\ G &= 1 - G \\ 2G &= 1 \\ G &= 0.5 \\ \end{aligned}

Now we have proved that $G = \frac{1}{2}$ !

Solving For H

Now that we’ve solved for $G$ , we can use it to solve $H$ . Here’s the answer for this:

\begin{aligned} H &= 1 - 2 + 3 - 4 + 5 ... \\ 2H &= 1 - 2 + 3 - 4 + 5 ... \\ &+ 0 + 1 - 2 + 3 - 4 ... \\ 2H \text{ } &\overline{= 1 - 1 + 1 - 1 + 1...} \\ 2H &= G \\ 2H &= 0.5 \\ H &= 0.25 \\ \end{aligned}

Now we have proved that $H = \frac{1}{4}$ !

Solving For S

Now that we’ve shows what $G$ and $H$ are equal to, it’s time to finally solve for $S$ .

\begin{aligned} S &= 1 + 2 + 3 + 4 + 5 + 6 ... \\ S - H &= 1 + 2 + 3 + 4 + 5 + 6 ... \\ &- 1 - 2 + 3 - 4 + 5 + 6 ... \\ S - H \text{ } &= 0 + 4 + 0 + 8 + 0 + 12 ... \\ S - H &= 4S \\ S - 0.25 &= 4S \\ -1/4 &= 3S \\ -1/12 &= S \\ \end{aligned}

Now we have proved that $S = -1/12$ , and we’re done!

Sources & Resources

I originally found out about this phenomenon at this YouTube video by Numberphile. It’s a great video and you should check it out.