Does Zero Equal One?

How to prove that 0 equals 1.

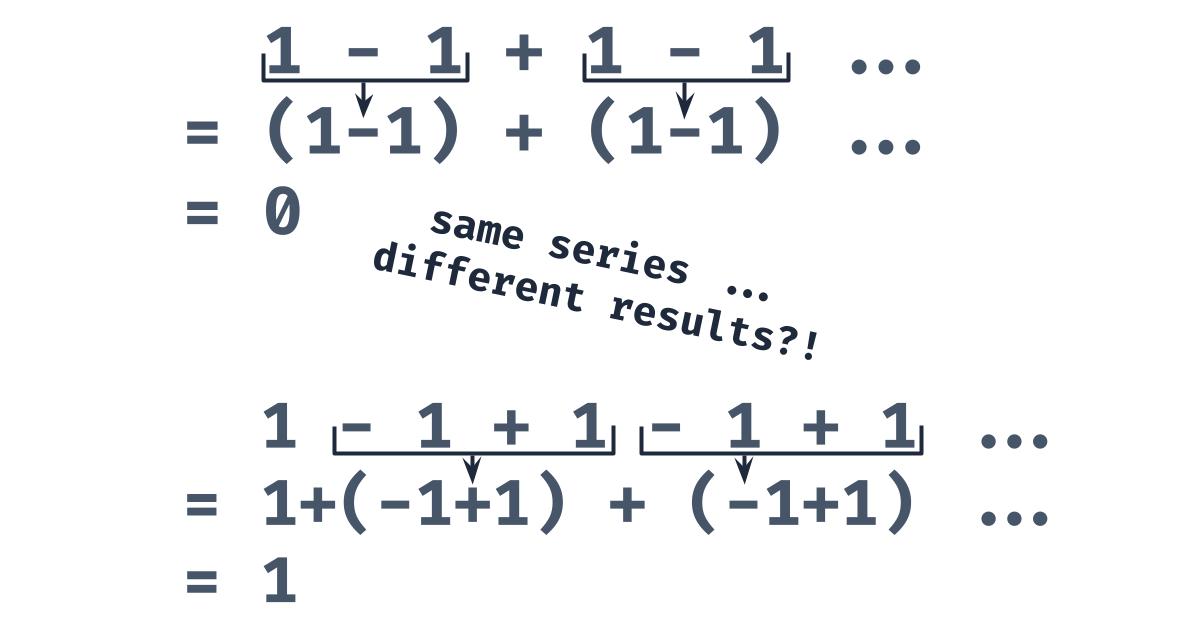
The “0 = 1” paradox states that the numbers 0 and 1 are equivalent. We can easily prove this. Once done, we’ll show you how you can use this to prove that any two numbers are equivalent!

DISCLAIMER: The math in this article is invalid, as we can’t abuse parentheses in a divergent series. It’s a fun experiment, but it doesn’t count as a valid argument.

We’ll start out with a series $S$ which we’ll prove to be equal to both 0 and 1. After that’s done, we can use basic mathematics to prove that 0 equals 1.

First of all, let’s define $S$ as follows:

S = 1 - 1 + 1 - 1 + 1 - 1...

Proving That S = 0

We can group the $1 - 1$ terms in $S$ into parentheses.

S = (1 - 1) + (1 - 1) + (1 - 1) + ...

Because $1 - 1 = 0$ , we can simplify this.

S = 0 + 0 + 0 + ...

Because we can add 0s forever and still get zero, we can simplify this even more.

S = 0

Ta da! We proved that $S = 0$ .

Proving That S = 1

We can group the $-1 + 1$ terms in $S$ into parentheses as well. Let’s try this.

S = 1 - (1 - 1) - (1 - 1) - (1 - 1) ...

Because $1 - 1 = 0$ , we can simplify this.

S = 1 - 0 - 0 - 0 ...

Because we can subtract 0s forever and still get zero, we can simplify this even more.

S = 1

Just like that, we proved that $S = 1$ .

Wait, S is 0 and 1?

Yup! Now we can use substitution to prove that $0 = 1$ .

\begin{aligned} S &= S \\ 0 &= S \\ 0 &= 1 \\ \end{aligned}

Proving That Any Two Numbers Are Equal

By multiplying both sides of the equation $0 = 1$ we can show that multiple numbers are equal to each other. For example, to prove that $5 = 98$ , we can use the following:

\begin{aligned} 0 &= 1 \text{ (proven already)} \\ 0 &= 5 \text{ (multiplying)} \\ 0 &= 98 \text{ (multiplying)} \\ 0 &= 5 \text{ (proven already)} \\ 98 &= 5 \text{ (substitution)} \\ \end{aligned}

And just like that, we’ve proved that $5 = 98$ !